Step

In the right triangle ADB
Find the length of the segment AB
Applying the Pythagorean Theorem
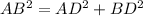
we have

substitute the values
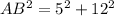

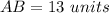
Step
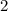
In the right triangle ADB
Find the cosine of the angle BAD
we know that

Step

In the right triangle ABC
Find the length of the segment AC
we know that
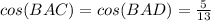
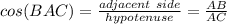


solve for AC

Step
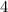
Find the length of the segment DC
we know that
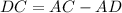
we have
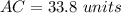
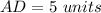
substitute the values
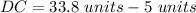
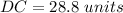
Step
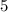
Find the length of the segment BC
In the right triangle BDC
Applying the Pythagorean Theorem
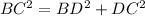
we have
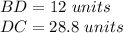
substitute the values

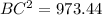

therefore
the answer is
