Answer:
Option D.
Step-by-step explanation:
Formula for amount after compound interest:
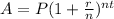
where,
P is principal
r is rate of interest.
n is number of times interest compounded in one period.
t is number of periods.
Given information:
P = $200
r = 2%=0.02
t = 3
n= 1
Substitute these values in the above formula.
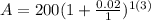
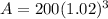
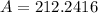
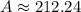
Keith have $212.24 in his account after three years.
Therefore, the correct option is D.