Question

What is the length of line segment Segment JK?

Answer 1

I did most of the math, but you would use the Pythagorean theorem. The answer should be the square root of 52.

Answer 2

The length of line segment JK is 2√13.

Explanation:

Consider the provided graph.

From the provided graph we can identify, the coordinate of k is (1, 2) and the coordinate of j is (-3, -4).

To find the distance between the line segment use the distance formula.

`D=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

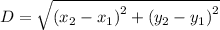
Substitute the respective values in the above formula.

`d=√(\left(-3-1\right)^2+\left(-4-2\right)^2)`

`d=√(\left(-4)^2+\left(-6)^2)`

`d=√(16+36)`

`d=√(52)`

`d=2√(13)`

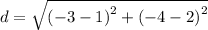
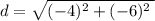
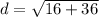
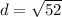
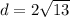
Hence, the length of line segment JK is 2√13.