Question

The focus of a parabola is (−5,−1) and the directrix is y=−3.

What is an equation of the parabola?

(x+5)² = 2(y + 5)

(x+5)² = y + 2

(x+5)² = 4(y + 2)

(x+5)² = 8(y + 5)

Explain Your Answer Please, Thank You

Answer 1

(x+5)^2=4(y+2)

Explanation:

Answer 2

`(x+5)^2=4(y+2)`

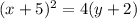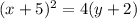
the equation for a parabola with focus (h, k+p) and directrix y=k-p is

`(x-h)^2=4p(y-k)`

so using your directrix y=-3, and knowing directrix is y=k-p, you have
-3=k-p.
similarly, knowing the focus is defined by (h,k+p) and your focus is (-5,-1)
you have the equation -1=k+p.

you now have a system of equations

`-3=k-p \\ -1=k+p`
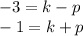
which you can solve using any method, I will use elimination.
adding down

`-4=2k \\ -2=k`
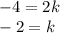
you now have k and can find p using either equation.

`-3=k-p \\ -3=-2-p \\ -1=-p \\ 1=p`.

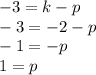
now you plug those in, getting the answer

`(x+5)^2=4(y+2)`