Answer:
The surface area of smaller solid is:
196 m^2
Explanation:
We know that for two similar solids:
One with surface area S and Volume V and the other with surface area S' and Volume V' is related by the formula as:
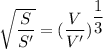
We have:
S=576 m^2
V=1728 m^3 and V'=343 m^3
Hence, the equation is written as:
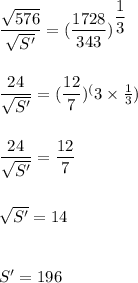
Hence, the surface area of smaller solid is:
196 m^2