Question

The volumes of two similar solids are 1,728 m3 and 343 m3. the surface area of the larger solid is 576 m2. what is the surface area of the smaller solid?

Answer 1

I just took this test, the answer is 196 m^2, I got it right

Answer 2

The surface area of smaller solid is:

196 m^2

Explanation:

We know that for two similar solids:

One with surface area S and Volume V and the other with surface area S' and Volume V' is related by the formula as:

`\sqrt{(S)/(S')}=((V)/(V'))^(1)/(3)`

We have:

S=576 m^2

V=1728 m^3 and V'=343 m^3

Hence, the equation is written as:

`(√(576))/(√(S'))=((1728)/(343))^{(1)/(3)}\\\\\\(24)/(√(S'))=((12)/(7))^(3* (1)/(3))\\\\\\(24)/(√(S'))=(12)/(7)\\\\\\√(S')=14\\\\\\S'=196`

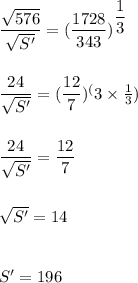
Hence, the surface area of smaller solid is:

196 m^2