
-intercepts occur at points
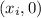
, so it follows that setting
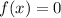
and solving for

will give you the

-coordinate of an intercept.
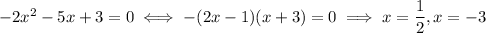
So the two intercepts are
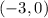
and
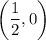
. For values of

between the two intercepts, say at
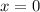
, you have
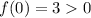
, which means the bounded region lies above the

-axis.
The area of the bounded region is then given explicitly by the definite integral
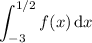
Barring that (given your "no calc explanations allowed" caveat), the best you can do is to approximate the area of the region with basic shapes.