Question

A problem that you will encounter in calculus 2 is finding the area under a curve. for the function f(x=-2x2-5x+3

a. find the x intercepts
b. describe how you would go about finding the area bounded by the x axis on the bottom and the x intercepts. calculus explanations not allowed.

Answer 1

`x`-intercepts occur at points
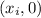
`(x_i,0)`, so it follows that setting
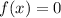
`f(x)=0` and solving for
`x` will give you the
`x`-coordinate of an intercept.


`-2x^2-5x+3=0\iff-(2x-1)(x+3)=0\implies x=\frac12,x=-3`

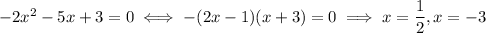
So the two intercepts are
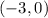
`(-3,0)` and
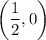
`\left(\frac12,0\right)`. For values of
`x` between the two intercepts, say at
`x=0`, you have
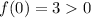
`f(0)=3>0`, which means the bounded region lies above the
`x`-axis.

The area of the bounded region is then given explicitly by the definite integral


`\displaystyle\int_(-3)^(1/2)f(x)\,\mathrm dx`

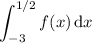
Barring that (given your "no calc explanations allowed" caveat), the best you can do is to approximate the area of the region with basic shapes.