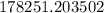Question

Myra took out a 20 year loan for $80,000 at an APR of 11.5% compounded monthly, approximately what would be the total cost of her loan if she paid it off 13 years early?

Answer 1

well, if she were to pay it 13years earlier, that means 20 - 13, or in 7years, so the monthly compounding will only apply to the 7years

thus


`\bf \qquad \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{compounded amount}\\ P=\textit{original amount deposited}\to &\$80000\\ r=rate\to 11.5\%\to (11.5)/(100)\to &0.115\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus 12 times} \end{array}\to &12\\ t=years\to &7 \end{cases} \\\\\\ A=80000\left(1+(0.115)/(12)\right)^(12\cdot 7)`

Answer 2

`178251.203502`

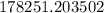
Explanation:

We have given:

Principal amount which is 80,000

Time which is 20 year

Rate which is 11.5%

And since, we have to find 13 years early so, time would be: 20-13=7 years.

And since, we have to find for 12 months

Hence, n=12

We have formula to calculate compound interest:

`P{1+(r)/(n)}^(nt)`

On substituting the values we get:

`80,000(1+(0.115)/(12))^(12\cdot 7)`

`\Rightarrow 80,000(1+((.115)/(12)})^(84)`

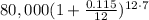
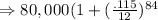
On simplification we get:

`178251.203502`