Question

What is the area of triangle GHJ?

Answer 1

Option B is correct.

The area of triangle GHJ is, 6 square units.

Step-by-step explanation:

Given: In ΔGHJ

the coordinates are G=(1,1) , H=(4,1) and J=(4,5).

Now, find the length of GH and HJ by using distance(D) formula for two points
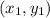`(x_1 ,y_1)` and
`(x_2 ,y_2)` is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

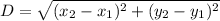
Calculate the length of GH;

GH =
`√((x_2-x_1)^2+(y_2-y_1)^2)` =
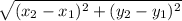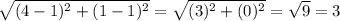`√((4-1)^2+(1-1)^2)= √((3)^2+(0)^2)=√(9) =3` unit

Similarly, for the length of HJ;

HJ =
`√((x_2-x_1)^2+(y_2-y_1)^2)` =
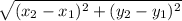`√((4-4)^2+(5-1)^2)= √((0)^2+(4)^2)=√(16) =4` unit

Using formula for the area of a triangle is

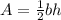`A=(1)/(2)bh`; where b is the base and h is the height.

then; the area of triangle GHJ;
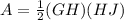`A=(1)/(2) (GH)(HJ)` where GH represents the base and HJ represents the height.

Substituting the values of GH and HJ in above formula:

`A=(1)/(2) \cdot 3 \cdot 4 =3 \cdot 2 =6` square units.

Therefore, the area of ΔGHJ is, 6 square units.

Answer 2

We are tasked to solve for the area of the triangle GHJ. The formula for solving the area of a triangle is Area = 1/2bh where b is the base measurement and h is the height measurement.
Based on the attached picture, the following are the measurements:
b = 3 units
h = 4 units

Solving for the area, we have:
Area = 1/2*3*4
Area = 6 squared units

The answer is the letter "B" or the second item in the choices.