Question

In one town, 39% of all voters are Democrats. If two voters are randomly selected for a survey, find the probability that they are both Democrats. Round to the nearest thousandth if necessary.

Answer 1

So you would do .39 times .39
that is .1521
If you round it is .152
.152 times 100 equals 15.2%

Answer 2

The probability is 0.152

Explanation:

We know that in this town 39% of all voters are Democrats. Therefore, the probability of a randomly selected voter being a Democrat is
`p=0.39`

The experiment of randomly select voters for a survey is called a Bernoulli experiment (under some suppositions). We suppose that exist independence in this randomly selection of voters. We also suppose that there are only two possibilities for the voter : It is Democrat or not.

Now the variable X : ''The randomly selected voter for a survey is Democrat'' is a Binomial random variable.

X ~ Bi (n,p)

The probability function for the BInomial random variable X is :

`P(X=x)=(nCx).p^(x).(1-p)^(n-x)`

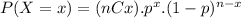
Where ''n'' is the number of Bernoulli experiments (In this case n = 2 because we randomly selected two voters)

P(X=x) is the probability of the variable X to assumes the value x

(nCx) is the combinatorial number define as

`(nCx)=(n!)/(x!(n-x)!)`

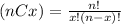
p = 0.39 in this exercise.

We are looking for P(X=2) ⇒

`P(X=2)=(2C2).(0.39)^(2).(1-0.39)^(2-2)=(0.39)^(2)=0.1521`

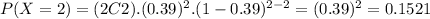
If we round to the nearest thousandth the probability is 0.152