Answer:
4.643 seconds
Explanation:
We have been given that
s = 6 feet
v = 73 feet per second
Substituting these values in the formula
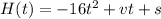
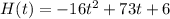
When the ball hits the ground, the height becomes zero. Thus, H(t)=0

We solve the equation using quadratic formula
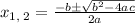
Substituting the values
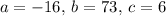
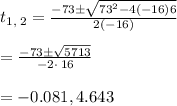
time can't be negative. Hence, t = 4.643.
Hence, the ball will take 4.643 seconds to hit the ground.