Question

Khalid wrote the sequence below.

x-1, -2x+2, 4x-4, -8x+8

Which formula can be used to find the 10th term of the sequence?
A. a10=(x-1)*(-2)^10-1
B. a10=(x-1)^10-1
C. a10=(x-1)*(2)^10-1
D. a10=(x-1)*(-2)^10

Answer 1

Formula A can help you find the 10th term.
I hope this Helps you

Answer 2

ANSWER

The 10th term of the sequence can be found using the formula,


`a_(10) =(x - 1)( - 2) ^( 10- 1)`

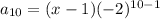
Step-by-step explanation

The first four terms of the geometric sequence were given as,


`(x-1),(-2x+2),(4x-4),(-8x+8)`

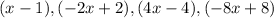
We can determine the common ratio using any two subsequent terms.

The common ratio is,

`r= ( - 2x + 2)/(x - 1)`

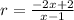
This implies that,

`r= ( - 2(x - 1))/(x - 1) = - 2`

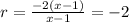
Also, the first term of the sequence is,


`a_1=x - 1`

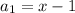
The general term of the sequence is given by,


`a_n=a_1(r) ^( n- 1)`

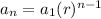
We substitute the first term, the common ratio and
`n= 10`
in to the general term to get,


`a_(10) =(x - 1)( - 2) ^( 10- 1)`

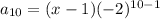
The correct answer is option A.