ANSWER
The 10th term of the sequence can be found using the formula,
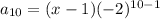
Step-by-step explanation
The first four terms of the geometric sequence were given as,
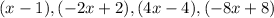
We can determine the common ratio using any two subsequent terms.
The common ratio is,
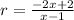
This implies that,
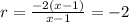
Also, the first term of the sequence is,
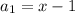
The general term of the sequence is given by,
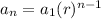
We substitute the first term, the common ratio and

in to the general term to get,
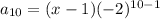
The correct answer is option A.