Answer:
A) 143.24
Explanation:
Here we have to use arc length of a circle formula.
Arc length =
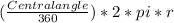
From this formula, we can drive central angle.
Central angle = (Arc length *360)/2πr
Given: Arc length = 10; r =4 and π = 3.14159
Plug in the given values in the above formula, we get
Central angle =

= 3600/25.13
Central angle = 143.24
Therefore, answer A) 143.24