Question

F=f (1-v/s) change the subject of the formula into v

Answer 1

Changing the subject of the formula into v means expressing v in terms of the other given variables. So given the original equation, as shown below, we can rearrange it so that we have v isolated on one side.


`F = f(1 - (v)/(s))`

`(F)/(f) = 1 - (v)/(s)`

`(v)/(s) = 1 - (F)/(f)`

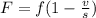
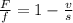
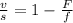
To isolate v, we can just multiply s to both sides and come up with the final equation below.


`v = s(1 - (F)/(f))`

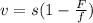
Thus, we have v = s(1 - F/f) with v as the subject of the formula.

Answer: v = s(1 - F/f)