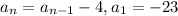Answer:
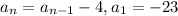
A is the correct option.
Explanation:
We have been given that
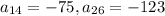
The general term of an arithmetic sequence is given by
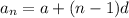
Now, for 14th term,
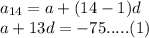
Similarly, for 26th term
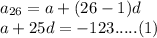
Subtract equation 1 and 2
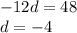
From equation 1
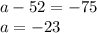
Hence, the first term is
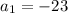
Now, since the common difference d is -4.
Hence, the recursive formula is