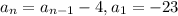Question

In an arithmetic sequence, a14=-75 and a26=-123 Which recursive formula defines the sequence?

A. an=an-1-4;a1=-23
B. an=an-1-4;a1=-19
C. an=-4an-1-19;a1=-23
D. an=-4an-1-19;a1=-19

Answer 1

`a_n=a_(n-1)-4,a_1=-23`

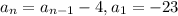
A is the correct option.

Explanation:

We have been given that
`a_(14)=-75,a_(26)=-123`

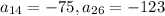
The general term of an arithmetic sequence is given by

`a_n=a+(n-1)d`

Now, for 14th term,

`a_(14)=a+(14-1)d\\a+13d=-75.....(1)`

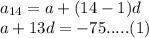
Similarly, for 26th term

`a_(26)=a+(26-1)d\\a+25d=-123.....(1)`

Subtract equation 1 and 2

`-12d=48\\d=-4`

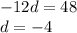
From equation 1

`a-52=-75\\a=-23`

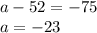
Hence, the first term is
`a_1=-23`

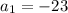
Now, since the common difference d is -4.

Hence, the recursive formula is

`a_n=a_(n-1)-4,a_1=-23`