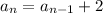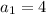Answer:
Option C is correct.
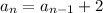
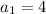
Explanation:
The arithmetic sequence says that:
For any sequence
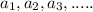
the recursive formula for this sequence is given by:
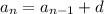
where d represents the common difference of two consecutive terms and n is the number of terms.
Give the pattern in the figure:
for n = 1,
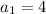
for n = 2,
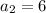
for n = 3,
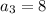
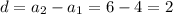 or
or
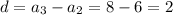
Now, substitute d =2 in the above formula we get;
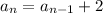
Therefore, recursive formula describes the patterns in the perimeter of the images is: