Question

In parallelogram ABCD, what is DC?

DC = in.

Answer 1

the answer is 13 inches

Explanation:

Answer 2

Since ABCD is a parallelogram, line AB and line DC are parallel and has the same value.

To solve this, equate line AB to be equal with line DC.
So,
Line AB = Line DC
(9x-14)in = (3x +4)in
Next group like terms to get the value of x
9x in-3x in = 4in+14in

`(6x)/(6)` =
`(18in)/(6)`
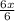
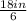
x = 3in

Since, we now have the value of x, substitute it to line DC’s equation.
DC=(3x+4)in
DC=(3(3) +4)in
DC=(9 +4) in
DC= 13 in

To check if the value is really correct, substitute X to AB
AB=(9x -14)in
AB=(9(3)-14)in
AB=(27-14)in
AB=13 in