Answer:
The total amount accrued, principal plus interest, from compound interest on an original principal of $ 2600 at a rate of 7% per year compounded 1 time per year over 13 years is $ 6266.
Explanation:
Given
Principle P = $2600
Interest rate r = 7% = 0.07
Time period t = 13 years
Compounded annually means: n = 1
To determine
Accrued Amount = ?
Using the formula
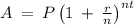
substituting P = 2600, r = 0.07, t = 13, n = 1
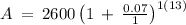
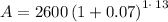
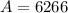 $
$
Therefore, the total amount accrued, principal plus interest, from compound interest on an original principal of $ 2600 at a rate of 7% per year compounded 1 time per year over 13 years is $ 6266.