Question

Drag and drop a phrase to make the statement true.

triangles ABC and DEF are...
A.) Similar
B.Not Similar

Answer 1

A similar because all triangles add up to 180 ,

they both have 80 so leaves 100 degrees left..

and they both have the same #'s 80, 60, & 40 degrees equal to 180 degrees

Answer 2

Answer: The answer is (A). Similar.

Step-by-step explanation: We are given two triangles, ΔABC and ΔDEF where, ∠B = 80°, ∠C = 60°, ∠D = 40° and ∠E = 80°.

We are to check whether the two triangles are similar or not.

In ΔABC, we have

`\angle A+\angle B+\angle C=180^\circ\\\\\Rightarrow \angle A+80^\circ+60^\circ=180^\circ\\\\\Rightarrow \angle A=180^\circ-140^\circ\\\\\Rightarrow \angle A=40^\circ,`

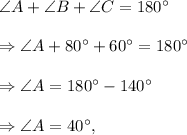
and in ΔDEF, we have

`\angle D+\angle E+\angle F=180^\circ\\\\\Rightarrow 40^\circ+80^\angle F=180^\circ\\\\\Rightarrow \angle F=180^\circ-120^\circ\\\\\Rightarrow \angle F=60^\circ.`

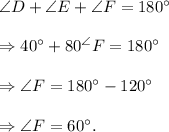
Therefore, in ΔABC and ΔDEF, we have

∠A = ∠D,

∠B = ∠E,

∠C = ∠F.

So, by AAA similarity postulate, we get

ΔABC ≈ ΔDEF.

Thus, (A) is the correct option.