Question

The half-life of the element radon (Rn86) is 3.8 days. In a sample originally containing 1 gram of radon, the amount of left over days is given by the model () = (0.5)t/3.8 a) How much radon will be present after 7.6 days? b) How much radon will be present after 10 days?

Answer 1

a.0.25 g

b.0.16 g

Explanation:

We are given that

Half-life of the element radon=3.8 days

Mass of sample of radon=1 g

The amount of radon left after t days is given by

`A(t)=(0.5)^{(t)/(3.8)}`

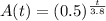
a.

We have to find the amount of radon left after 7.6 days.

Substitute t=7.6 in the equation

Then, we get

`A(7.6)=(0.5)^{(7.6)/(3.8)}`

`A(7.6)=0.25 g`

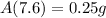
Hence, the amount of radon will be present after 7.6 days=0.25 g

b. We have to find the amount of radon left after 10 days.

Substitute t=10 in the equation

Then, we get

`A(10)=(0.5)^{(10)/(3.8)}`

`A(10)=0.16g`

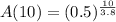
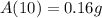
Hence, the amount of radon will be present after 10 days=0.16 g