Question

Figure A is a cylinder. Figure B is a cone. The figures have the same height and the circular bases have the same diameter. Which statement is true? A) The volume of A is 2 times the volume of B B) The volume of the cone is equal to the volume of the cylinder. C) The base of the cone and the top of the cylinder have the same area. D) The surface area of the cylinder and the surface area of the cone are equal.

Answer 1

The cone has the smallest volume of the 2 figures. This is because formula for cylinder is b x h, the formula for cone is 1/3(b x h) so if they have same height and base area cylinder would have larger volume because for cylinder, formula is one-third of b x h. Hope I helped!! : )

Answer 2

C)The base of the cone and the top of the cylinder have the same area.

Explanation:

Given : Cylinder and Cone with same height and radius .

Solution :

Since height and radius is same of both cone and cylinder.

Volume of cone is
`(1)/(3)\pi r^(2) h`

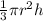
Volume of cylinder is
`\pi r^(2)h`

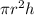
Thus the volume of cone is 1/3 rd the volume of cylinder having same radius and height.

Thus Option A and B is wrong

Option C )The base of the cone and the top of the cylinder have the same area.

Since radius is same

Base of cone =
`\pi r^(2)`

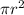
Base of cylinder =
`\pi r^(2)`

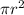
refer attached file .

Thus Option C is correct

Option D : The surface area of the cylinder and the surface area of the cone are equal.

Since height an radius is same

Thus the surface area of cone is
`\pi r^(2) + \pi r \sqrt{h^(2)+ r^(2) }`

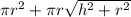
Surface area of cylinder is
`2\pi rh +2\pi r^(3)`

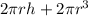
Thus areas are not equal

Hence Option D is wrong .