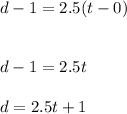Question

Two objects are moving along separate linear paths where each path is described by position, d, and time, t. The variable d is measured in meters, and the variable t is measured in seconds. The equation describing the graph of the position of the first object with respect to time is d = 2.5t + 2.2. The graph of the position of the second object is a parallel line passing through (t = 0, d = 1). What is the equation of the second graph?

Answer 1

I am not sure about this but here goes nothing: d=2.5t+2.2 is very familiar to y=mx+b y=d m=2.5 x=t b=2.2 to find a new quasion we substitute d and t into place wich equals 1=2.5(0)+b simplification and you get b=1 so your answer is d=2.5t+1

Answer 2

The equation of the second graph is:

`d=2.5t+1`

Explanation:

We know that the slope of a line parallel to a given line is equal to the slope of that line.

Here the slope of the second line=2.5

( Since, first line has slope=2.5 )

Also, we know that the equation of a line passing through (a,b) and slope m is given by:

`y-b=m(x-a)`

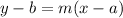
Here (a,b)= (0,1) and m=2.5 , y=d and x=t

Hence, the equation of second line is given by:

`d-1=2.5(t-0)\\\\\\d-1=2.5t\\\\d=2.5t+1`