By inspection, it's clear that the sequence must converge to

because
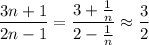
when

is arbitrarily large.
Now, for the limit as
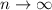
to be equal to

is to say that for any
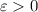
, there exists some
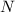
such that whenever
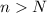
, it follows that
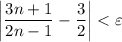
From this inequality, we get
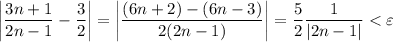
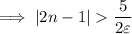
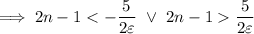
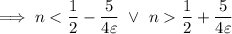
As we're considering
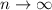
, we can omit the first inequality.
We can then see that choosing
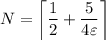
will guarantee the condition for the limit to exist. We take the ceiling (least integer larger than the given bound) just so that
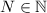
.