Question

In the xy-coordinate plane, the graph of the equation y=2x^2-12x-32 has zeros at x=d and x=e, where d>e. The graph has a minimum at (f,-50) what are the vaules of d,e,and f?

Answer 1

to find the zeroes solve fro x:-

2(x^2 - 6x - 16) = 0

2(x - 8)(x + 2) = 0

x = {8, -2
so d = 8 and e = -2

the x coordinate of the minimum value = - b / 2a = 12/ 2*2 = 3

f = 3

Answer 2

Answer: The values are d = 8, e = - 2 and f = 3.

Step-by-step explanation: Given that in the xy-plane, the graph of the equation
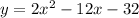`y=2x^2-12x-32` has zeros at x=d and x=e, where d > e. The graph has a minimum at (f, -50).

We are to find the values of d, e and f.

The zeroes of the given function are

`2x^2-12x-32=0\\\\\Rightarrow x^2-6x-16=0\\\\\Rightarrow x^2-8x+2x-16=0\\\\\Rightarrow x(x-8)+2(x-8)=0\\\\\Rightarrow (x-8)(x+2)=0\\\\\Rightarrow x-8=0,~~~~~x+2=0\\\\\Rightarrow x=8,~~~~~~~~\Rightarrow x=-2.`

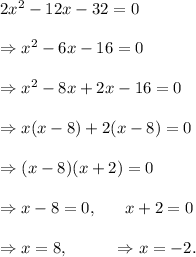
So, d = 8 and e = -2.

We know that the minimum value of a function
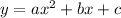`y=ax^2+bx+c` occurs at
`x=-(b)/(2a).`

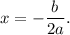
Therefore, the given function will have a minimum values at

`x=-(b)/(2a)=-(-12)/(2* 2)=(12)/(4)=3.`

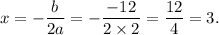
Therefore, the function has minimum at (3, -50) and so the value of f is 3.

Thus, d = 8, e = - 2 and f = 3.