Answer: The average rate of change is

Explanation:
Since we have given that
Two points are given below:
(-2,3) and (2,5)
As we know that Average rate of change of function = Slope of line passing through (-2,3) and (2,5)
So, Slope of line is given by
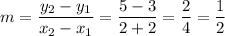
Hence, the average rate of change is
