The function f(x) = 0.11(3)x is reflected over the x-axis to produce function g(x). Function g(x) is then reflected over the y-axis to produce function h(x). Which function repr…

Question

asked Jul 1, 2018 119k views

2 Answers

Taylonr · Answer 1 · 2018-07-06T10:48:10+0000

Answer:

Option d is correct

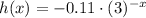
$h(x) = -0.11 \cdot (3)^(-x)$

Explanation:

Given the function:

$f(x) = 0.11 \cdot 3^x$

First find the function g(x) when f(x) is reflected over the x-axis.

The rule of reflection across x-axis is given by:

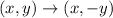
$(x, y) \rightarrow (x, -y)$

then;

Apply the rule of reflection across x-axis on f(x) we get,

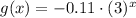
$g(x)=-0.11 \cdot (3)^(x)$

Now, function g(x) is then reflected over the y-axis to produce function h(x).

The rule of reflection across y-axis is given by:

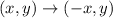
$(x, y) \rightarrow (-x, y)$

then;

Apply the rule of reflection across y-axis on g(x) we get,

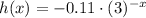
$h(x) = -0.11 \cdot (3)^(-x)$

Therefore,
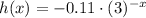$h(x) = -0.11 \cdot (3)^(-x)$ function represents h(x)