Answer:
Option d is correct
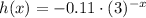
Explanation:
Given the function:
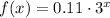
First find the function g(x) when f(x) is reflected over the x-axis.
The rule of reflection across x-axis is given by:
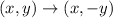
then;
Apply the rule of reflection across x-axis on f(x) we get,
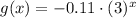
Now, function g(x) is then reflected over the y-axis to produce function h(x).
The rule of reflection across y-axis is given by:
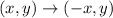
then;
Apply the rule of reflection across y-axis on g(x) we get,
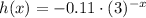
Therefore,
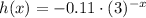 function represents h(x)
function represents h(x)