Question

Find the height of a square pyramid that has a volume of 12 cubic feet and a base length of 3 feet

Answer 1

`\bf \textit{volume of a pyramid}\\\\ V=\cfrac{1}{3}Bh\qquad \begin{cases} B=\textit{base area}\\ h=height\\ ----------\\ B=3\\ V=12 \end{cases}\implies 12=\cfrac{1}{3}\cdot 3h`

solve for "h"

Answer 2

Volume(V) of a right square pyramid is given by:

`V = (1)/(3) a^2h`

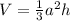
where,

a is the base length and h is the height respectively.

As per the statement:

A square pyramid that has a volume of 12 cubic feet and a base length of 3 feet.

⇒V = 12 cubic feet and a = 3 feet

Substitute these in [1] we have';

`12 = (1)/(3) \cdot 3^2 \cdot h`

⇒
`12 = (1)/(3) \cdot 9 \cdot h`

⇒
`12 = 3 \cdot h`

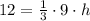
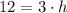
Divide both sides by 3 we have;

4 = h

or

h = 4 feet

Therefore, the height of of a square pyramid is, 4 feet