Question

Two sets of equatic expressions are shown below in various forms: Line 1: x2 + 3x + 2 (x + 1)(x + 2) (x + 1.5)2 − 0.25 Line 2: x2 + 5x + 6 (x + 2)(x + 3) (x + 2.5)2 + 6.25 Which line contains three equivalent expressions?

Answer 1

Line 1: x2 + 3x + 2 (x + 1)(x + 2) (x + 1.5)2 − 0.25

Explanation:

Answer 2

Answer: The correct line is

`\textup{Line 1 :}x^2+3x+2=(x+1)(x+2)=(x+1.5)^2-0.25.`

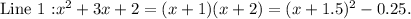
Step-by-step explanation: We are given the following two sets of quadratic expressions in various forms:

`\textup{Line 1: }x^2+3x+2=(x+1)(x+2)=(x+1.5)^2-0.25,\\\\\textup{Line 2 :}x^2+5x+6=(x+2)(x+3)=(x+2.5)^2+6.25.`

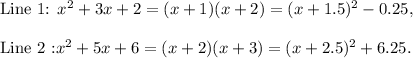
We are to select one of the lines from above that represent three equivalent expressions.

We can see that there are three different forms of a quadratic expression in each of the lines:

First one is the simplified form, second is the factorised form and third one is the vertex form.

So, to check which line is correct, we need to calculate the factorised form and the vertex form from the simplified form.

We have

`\textup{Line 1: }\\\\x^2+3x+2\\\\=x^2+2x+x+2\\\\=x(x+2)+1(x+2)\\\\=(x+1)(x+2),`

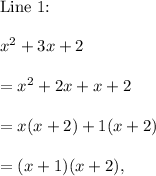
and

`x^2+3x+2\\\\=x^2+2* x* 1.5+(1.5)^2-(1.5)^2+2\\\\=(x+1.5)^2-2.25+2\\\\=(x+1.5)^2-0.25.`

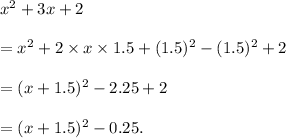
So,

`\textup{Line 1 :}x^2+3x+2=(x+1)(x+2)=(x+1.5)^2-0.25.`

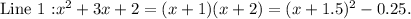
Thus, Line 1 contains three equivalent expressions.

Now,

`\textup{Line 2: }\\\\x^2+5x+6\\\\=x^2+3x+2x+6\\\\=x(x+3)+2(x+3)\\\\=(x+2)(x+3),`

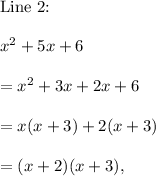
and

`x^2+5x+6\\\\=x^2+2* x* 2.5+(2.5)^2-(2.5)^2+6\\\\=(x+2.5)^2-6.25+6\\\\=(x+2.5)^2-0.25\\eq (x+2.5)^2+6.25.`

So,

`\textup{Line 2 :}x^2+3x+2=(x+1)(x+2)=(x+1.5)^2+6.25.`

Thus, Line 2 does not contain three equivalent expressions.

Hence, Line 1 is correct.