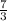What is the solution of log3x − 2125 = 3

Question

asked Nov 7, 2018 214k views

2 Answers

Valdemar · Answer 1 · 2018-11-13T17:32:12+0000

Answer:

The solution for the given expression
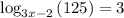$\log _(3x-2)\left(125\right)=3$ is

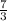
Explanation:

Given : Expression
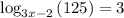
$\log _(3x-2)\left(125\right)=3$

We have to find the solution for the given expression
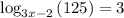
$\log _(3x-2)\left(125\right)=3$

Consider the given expression
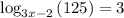
$\log _(3x-2)\left(125\right)=3$

Apply log rule,
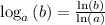
$\log _a\left(b\right)=(\ln \left(b\right))/(\ln \left(a\right))$

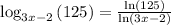
$\log _(3x-2)\left(125\right)=(\ln \left(125\right))/(\ln \left(3x-2\right))$

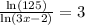
$(\ln \left(125\right))/(\ln \left(3x-2\right))=3$

Multiply both side by
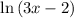
$\ln \left(3x-2\right)$

We get,
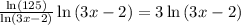
$(\ln \left(125\right))/(\ln \left(3x-2\right))\ln \left(3x-2\right)=3\ln \left(3x-2\right)$

Simplify , we have,

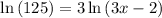
$\ln \left(125\right)=3\ln \left(3x-2\right)$

Divide both sie by 3, we get,

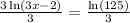
$(3\ln \left(3x-2\right))/(3)=(\ln \left(125\right))/(3)$

Also,
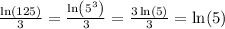
$(\ln \left(125\right))/(3)=(\ln \left(5^3\right))/(3)=(3\ln \left(5\right))/(3)=\ln(5)$

Thus,
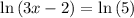
$\ln \left(3x-2\right)=\ln \left(5\right)$

When logs have same base, we have,

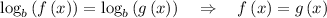
$\log _b\left(f\left(x\right)\right)=\log _b\left(g\left(x\right)\right)\quad \Rightarrow \quad f\left(x\right)=g\left(x\right)$

Thus,
3x - 2 = 5

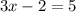
Add 2 both sides, we have,

3x = 7

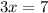
Divide both side by 3, we have,

x=(7)/(3)

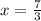
Thus, the solution for the given expression
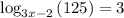$\log _(3x-2)\left(125\right)=3$ is