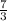Answer:
The solution for the given expression
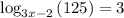 is
is
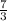
Explanation:
Given : Expression
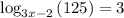
We have to find the solution for the given expression
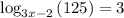
Consider the given expression
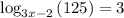
Apply log rule,
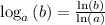
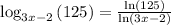
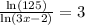
Multiply both side by
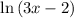
We get,
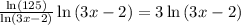
Simplify , we have,
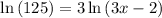
Divide both sie by 3, we get,
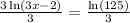
Also,
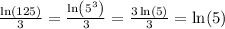
Thus,
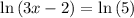
When logs have same base, we have,
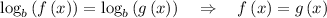
Thus,
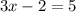
Add 2 both sides, we have,
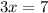
Divide both side by 3, we have,
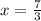
Thus, the solution for the given expression
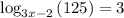 is
is