Answer:
Vertex is minimum.
Coordinate is (3,5)
Explanation:
Given :
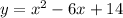
To find : Complete the square to rewrite in vertex form. Then state whether the vertex is a maximum or minimum and give its coordinates.
Solution :
The general vertex form is

where (h,k) is the vertex of the function
Converting into vertex form by completing the square,
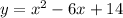
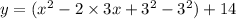
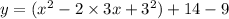

This is the vertex form where a=1, (h,k)=(3,5)
If a>0 then vertex is minimum
If a<0 then vertex is maximum.
In our case, 1>0 then vertex is minimum.
Coordinates is (3,5).