Answer:
A. It is stretched vertically by a factor of 3.
Explanation:
Given are two functions
f and g
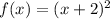
i.e. f is a parabola with vertex at (-2,0) open up
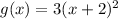
This is also a parabola with vertex at (-2,0) open up
g(x) = 3 f(x)
This means f(x) is smaller vertically than g(x)
Or f(x) is stretched vertically by a factor of 3 to get g(x)
Hence option A is true.
A. It is stretched vertically by a factor of 3.