Question

Find the diagonal of a square whose sides are of the given measure. Given = 5"

Answer 1

Use the Pythagorean Theorem. a = b = 5 so
5^2 + 5^2 = c^2
25 + 25 = c^2
50 = c^2
c = 5
`√(2)` = 7.071

Answer 2

Answer: The length of the diagonal of the square is 7.07 inches.

Step-by-step explanation: We are given to find the length of the diagonal of a square whose side is of measure 5 in.

As shown in the attached figure below, ABCD is a square, where

AB = BC = CD = DA = 5 in. and AC is one of the diagonals.

Since all the four angles of a square are right-angles, so triangle ABC will be a right-angled at angle ABC.

So, the diagonal AC is the hypotenuse of the triangle.

Applying the Pythagoras theorem in the right-angled triangle ABC, we have

`AC^2=AB^2+BC^2\\\\\Rightarrow AC=√(5^2+5^2)\\\\\Rightarrow AC=√(25+25)\\\\\Rightarrow AC=√(50)\\\\\Rightarrow AC=5\sqrt2\\\\\Rightarrow AC=5* 1.4142\\\\\Rightarrow AC=7.07.`

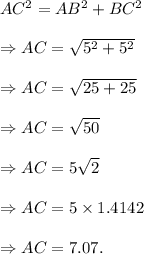
Thus, the length of the diagonal of the square is 7.07 inches.