Answer:
C.
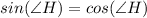
Explanation:
Givens
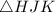 is a right triangle.
is a right triangle.
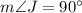
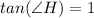
We this information, we can deduct that the opposite leg to
 is JK, and the adjacent leg to
is JK, and the adjacent leg to
 is JH. So, if
is JH. So, if
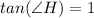 , this means that both legs are equal, because to result the tangent in 1, both legs have to be equal
, this means that both legs are equal, because to result the tangent in 1, both legs have to be equal
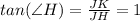
Also, we can deduct that the angle
 is equal to 45°, because when the tangent is equal to one unit, that means the triangle is symmetric, which means that its angles are 45°.
is equal to 45°, because when the tangent is equal to one unit, that means the triangle is symmetric, which means that its angles are 45°.
So, with knowing the measure of
 , we can find the rest of trigonometric reasons
, we can find the rest of trigonometric reasons
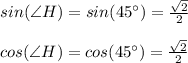
Basically, this means that both reasons are equal
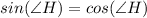
Therefore, the right answer is C.