Answer:
1. The amount due to Stan at the end of 5 year is $10,021.65
2. Maggie will get $22,883.01 after 7 years.
3. The current value of the investment is $73,947.52
Explanation:
1. We use the formula for compound interest which is compounded continuously
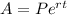
Where A = Amount
P = Principal amount ($5,500)
e = Mathematical constant e
r = rate of interest 12% ( 0.12)
t = Time in years (5)
Now we put the values:
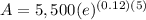
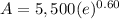
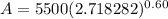
A = 5,500 × 1.8221188004
A = 10,021.653402147 ≈ $10,021.65
2. We will solve this question by the formula of compound interest.
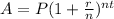
Where A = Amount
P = principal amount ($16,250)
r = rate of interest in decimal 4.9% (0.049)
n = time of compounding in a year (12)
t = time in years ( 7 )
Now put the values in formula
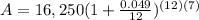
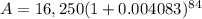
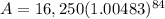
A = $22,883.01
3. In this question investment made in the stock market decreased at a rate of 1.2% per year for 25 years. so we use the formula
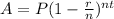
Now put the values in formula
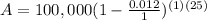
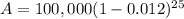
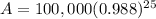
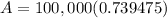
A = $73947.52
4. Similarities between saving money and investing money, in both you secure some money for future in other words both can help you a more comfortable financial future.
The difference is saving money is allows you to earn lower return but with no risk but investing money is allows you to earn higher return but you take on the risk of loss.