Question

FOUR QUESTIONS HELP PLEASE

1. Stan borrows $5,500 at a rate of 12% interest per year. What is the amount due at the end of 5 years if the interest is compounded continuously? In your final answer, include your calculations.

2. If Maggie invests $16,250 at a rate of 4.9%, compounded monthly, find the value of the investment after 7 years. Include your calculations in your final answer.

3. An investment made in the stock market decreased at a rate of 1.2% per year for 25 years. What is the current value of the $100,000 investment? Include your calculations in your final answer.

4. In two or more complete sentences explain the similarities and differences between saving money and investing money.

Answer 1

1. The amount due to Stan at the end of 5 year is $10,021.65

2. Maggie will get $22,883.01 after 7 years.

3. The current value of the investment is $73,947.52

Explanation:

1. We use the formula for compound interest which is compounded continuously

`A=Pe^(rt)`

Where A = Amount

P = Principal amount ($5,500)

e = Mathematical constant e

r = rate of interest 12% ( 0.12)

t = Time in years (5)

Now we put the values:

`A=5,500(e)^((0.12)(5))`

`A=5,500(e)^(0.60)`

`A=5500(2.718282)^(0.60)`

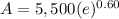
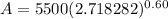
A = 5,500 × 1.8221188004

A = 10,021.653402147 ≈ $10,021.65

2. We will solve this question by the formula of compound interest.

`A=P(1+(r)/(n))^(nt)`

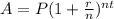
Where A = Amount

P = principal amount ($16,250)

r = rate of interest in decimal 4.9% (0.049)

n = time of compounding in a year (12)

t = time in years ( 7 )

Now put the values in formula

`A=16,250(1+(0.049)/(12))^((12)(7))`

`A=16,250(1+0.004083)^(84)`

`A=16,250 (1.00483)^(84)`

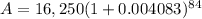
A = $22,883.01

3. In this question investment made in the stock market decreased at a rate of 1.2% per year for 25 years. so we use the formula

`A=P(1-(r)/(n))^(nt)`

Now put the values in formula

`A=100,000(1-(0.012)/(1))^((1)(25))`

`A=100,000(1-0.012)^(25)`

`A=100,000(0.988)^(25)`

`A=100,000(0.739475)`

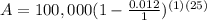
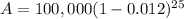
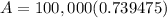
A = $73947.52

4. Similarities between saving money and investing money, in both you secure some money for future in other words both can help you a more comfortable financial future.

The difference is saving money is allows you to earn lower return but with no risk but investing money is allows you to earn higher return but you take on the risk of loss.

Answer 2

For questions 1-3, the formula used is A = P (1 + r/n) ^(nt).
1.) Without compound interest, you would earn only $8800.00. This means that thanks to the power of compound interest you will earn an additional $1191.83 in interest at the end of the 5 year term.
2.) Using the compounded interest formula, you will earn $22883.01 after the 7 year term.
3.) Because of the negative interest, the compounded amount is only $695,929.30.
4.) Putting money in a saving account is saving money with a lower earning compared to investments. Investments have the higher potential of earning more than just having a basic savings account.