Question

HELP!!! Determine if the graph is symmetric about the x-axis, the y-axis, or the origin. r = 4 cos 3θ

I don't think it's symmetric?

Answer 1

testing for y-symmetry let's make r = 5 cos 3θ and set θ=π−θ sor=5cos3θθ=(π−θ)r=5cos(3(π−θ))⟹r=5cos(3π−3θ)

Answer 2

The graph is symmetric about the x-axis.

Explanation:

• The graph is symmetric about the polar axis(x-axis) if we replace (r,θ) with (r,-θ) then it is equivalent to the original equation.

• The graph is symmetric about the y-axis if we replace (r,θ) with (-r,-θ) then it is equivalent to the original equation.

• The graph is symmetric about the pole(origin) if we replace (r,θ) with (-r,θ) then it is equivalent to the original equation.

Here we have equation as:

`r=4\cos 3\theta`

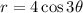
• when we replace (r,θ) with (r,-θ) we have:

`r=4\cos 3(-\theta)\\\\i.e.\\\\r=4\cos (-3\theta)\\\\i.e.\\\\r=4\cos 3\theta`

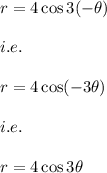
( Since, we know that:

`\cos (-\tehta)=\cos \theta` )

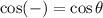Hence, the graph is symmetric about the x-axis.

• when we replace (r,θ) with (-r,-θ)

`-r=4\cos 3(-\theta)\\\\i.e.\\\\-r=4\cos (-3\theta)\\\\i.e.\\\\-r=4\cos 3\theta\\\\i.e.\\\\r=-4\cos 3\theta`

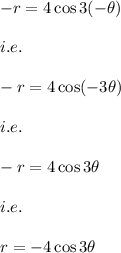
Hence, we observe that on replacing the function the two graphs are not equivalent.

Hence, the graph is not symmetric about the y-axis.

• when we replace (r,θ) with (-r,θ) we have:

`-r=4\cos 3\theta\\\\i.e.\\\\r=-4\cos 3\theta`

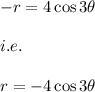
Hence, we observe that on replacing the function the two graphs are not equivalent.

Hence, the graph is not symmetric about the pole(origin)