Answer:
Question 5
We get n=42.15 and o=71.5
Question 6
We get e=15.32 and t=17.88
Explanation:
Question 5
The triangles are similar.
So, the ratio of corresponding sides will be similar.
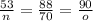
First we will solve
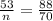 to find value of n.
to find value of n.
Cross multiply
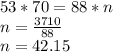
Now, we will solve
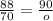 to find value of o
to find value of o
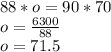
So, We get n=42.15 and o=71.5
Question 6
The triangles are similar.
So, the ratio of corresponding sides will be similar.
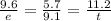
First we will solve
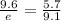 to find value of n.
to find value of n.
Cross multiply
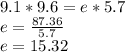
Now, we will solve
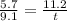 to find value of o
to find value of o
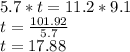
So, We get e=15.32 and t=17.88