Question

Mr. Walker gave his class the function f(x) = (x + 3)(x + 5). Four students made a claim about the function. Each student’s claim is below.

Jeremiah: The y-intercept is at (15, 0).
Lindsay: The x-intercepts are at (–3, 0) and (5, 0).
Stephen: The vertex is at (–4, –1).
Alexis: The midpoint between the x-intercepts is at (4, 0).
Which student’s claim about the function is correct?

Answer 1

On E2020 its Stephen is correct

Explanation:

Answer 2

Stephen's claim is correct.

Explanation:

The given function is

`f(x)=(x+3)(x+5)`

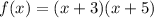
Put x=0 to find the y-intercepts.

`f(0)=(0+3)(0+5)=3* 5=15`

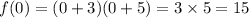
The y-intercept of the function is at (0,15). It means jeremiah's statement is incorrect.

Put f(x)=0, to find the x-intercept.

`0=(x+3)(x+5)`

`x+3=0\Rightarrow x=-3`

`x+5=0\Rightarrow x=-5`

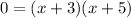
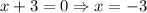
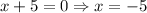
The x-intercepts are at (-3,0) and (-5,0). It means Lindsay's statement is incorrect.

`f(x)=(x+3)(x+5)`

`f(x)=x^2+8x+15`

`f(x)=x^2+8x+15+16-16`

`f(x)=(x^2+8x+16)-1`

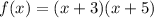
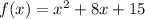
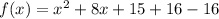
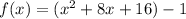
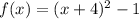`f(x)=(x+4)^2-1` .... (1)

The vertex form of a parabola is

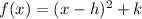`f(x)=(x-h)^2+k` .... (2)

Where, (h,k) is vertex.

From (1) and (2) it is clear that the vertex of the parabola is (-4,-1), Stephen's claim is correct.

The midpoint between the x-intercepts is

`((-3-5)/(2),(0+0)/(2))=(-4,0)`

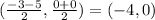
The midpoint between the x-intercepts is at (-4, 0). It means Alexis's statement is incorrect.