Answer:
Stephen's claim is correct.
Explanation:
The given function is

Put x=0 to find the y-intercepts.

The y-intercept of the function is at (0,15). It means jeremiah's statement is incorrect.
Put f(x)=0, to find the x-intercept.
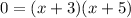
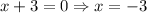
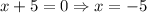
The x-intercepts are at (-3,0) and (-5,0). It means Lindsay's statement is incorrect.


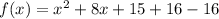

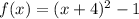 .... (1)
.... (1)
The vertex form of a parabola is
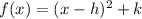 .... (2)
.... (2)
Where, (h,k) is vertex.
From (1) and (2) it is clear that the vertex of the parabola is (-4,-1), Stephen's claim is correct.
The midpoint between the x-intercepts is
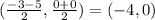
The midpoint between the x-intercepts is at (-4, 0). It means Alexis's statement is incorrect.