Question

The vertex of a parabola represented by f(x)=x^2 - 4x + 3 has coordinates (2,-1). Find the coordinates of the vertex of the parabola defined by g(x)=f(x-2). Explain how you arrived at your answer

Answer 1

`f(x)=x^2-4x+3`
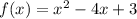
a=1, b=-4, c=3
If the vertex has coordinates (2;-1)(p=2,q=-1) we can write vertex form of a parabola equation:

`f(x)=a(x-p)^2+q`

`f(x)=1(x-2)^2-1`

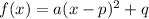
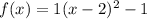
We need to put (x-2) at the place of (x) in f(x) equation to get g(x)

`g(x)=1[(x-2)-2]^2-1`

`g(x)=(x-2-2)^2-1`

`g(x)=(x-4)^2-1`
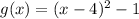
So:
p=4, q=-1

Vertex of the parabola defined by g(x)=f(x-2) has the vertex at
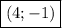
`\boxed{(4;-1)}`

:)