Answer: C. 433
Explanation:
Linear equation: y=mx+c, where m= constant rate of change, c=initial value of yor y-intercept.
Let x = number of years after 1914.
y= Number of stamps after x years.
In 1954 (year 40), there were 203 stamps in the collection.
i.e. 203=40m+c (i) [rate of change in number of stamps is constant]
In 1990 (year 76), there were 383 stamps in the collection.
i.e. 383=76m+c (ii)
Subtract (i) from (ii)
180= 36m
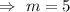 i.e. 5 stamps added per year.
i.e. 5 stamps added per year.
from (i),
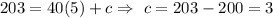 [Initially he has 3 stamps]
[Initially he has 3 stamps]
Stamps in 2000(year 86) = m(86)+c= 5(86)+3
= 430+3
= 433
Hence, correct option is C. 433