Question

Isaac is looking through binoculars on a whale watching trip when he notices a sea otter in the distance. If he is 20 feet above sea level in the boat, and the angle of depression is 30 degrees, how far away from the boat is the otter (to the nearest foot)?

Answer 1

tan of an angle = perpendicular / base
Here, perpendicular is the side of the triangle opposite the angle.
And base is the arm of the angle other the hypotenuse.

If the side of the triangle to be found (marked as ? in the figure) is x, then

perpendicular = 20 feet
base = x

so, tan 30 = 20/x
so, x = 20/(tan 30 degrees) = 34.64 feet
= 35 feet to the nearest foot

Answer 2

The otter is 34 feet from the boat, approximately.

Explanation:

The angle of depression is the angle formed by the horizontal and the line of sight. The image attached shows an example.

Now, as you can observe, the situation can be modeled by a right triangle, where we need to use trigonometric reasons to find the answer, the horizontal distance.

`tan30=(y)/(x)=(20)/(x) \\ x=(20)/(tan30) =(20)/(0.58)\\ x \approx 34`

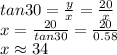
Therefore, the otter is 34 feet from the boat, approximately.