Question

Wilson has a balance of $890 on a credit card with an APR of 18.7%, compounded monthly. About how much will he save in interest over the course of a year if he transfers his balance to a credit card with an APR of 12.5%, compounded monthly? (Assume that Wilson will make no payments or new purchases during the year, and ignore any possible late-payment fees.)

Answer 1

890×(1+0.187÷12)^(12)−890×(1+0.125÷12)^(12)
=63.61 saved

Answer 2

He will save $ 63.61 ( approx ).

Explanation:

Since, the credit card balance formula,

`A=P(1+r)^t`

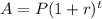
Where,

P = Original balance

r = rate per period,

t = number of periods,

If P = $ 890,

Annual interest rate = 18.7% = 0.187 ⇒ monthly rate, r =
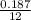`(0.187)/(12)` ( ∵ 1 year = 12 months )

Number of years = 1 ⇒ months, t = 12,

Thus, the balance after year,

`A_1=890(1+(0.187)/(12))^(12)\approx \$1071.46`

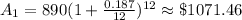
If Annual interest rate = 12.5% = 0.125 ⇒ monthly rate, r =
`(0.125)/(12)`

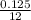
The balance would be,

`A_2=890(1+(0.125)/(12))^(12)\approx \$1007.85`

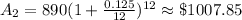
Since,

`A_1-A_2=1071.46-1007.85=\$ 63.61`

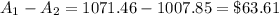
Hence, he will save $ 63.61 ( approx ).