Answer:
The correct option is A.
Explanation:
Given information: O is the center of the circle, and measure of angle C is 57°.
Alternate segment theorem: According to the alternate segment theorem an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Line RD is tangent to the circle at point D.
Using alternate interior theorem,
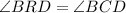
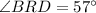
![[\because C=57^(\circ)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/xh2g73oalv11a05cvcd5v9i47dk2dhd7hg.png)
Therefore option A is correct.