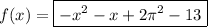Integrate by parts to find some useful recurrences relating Iₙ and Jₙ.
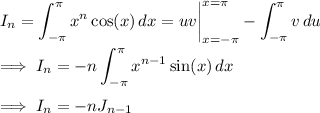
where u = xⁿ and dv = cos(x) dx.
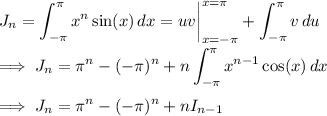
The integrals for n = 0 are trivial:
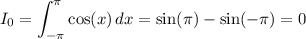
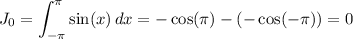
Now, the integral we're interested in is
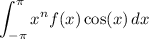
but we know f(x) is quadratic, and we want to find its coefficients a, b, and c such that
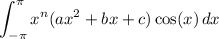
But this is simply
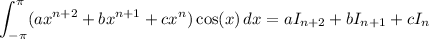
Using the recurrences above and the initial values we've computed, we find
• I₁ = -J₀ = 0
• J₁ = π - (-π) + I₀ = 2π
• I₂ = -2 J₁ = -4π
• J₂ = π² - (-π)² + 2 I₁ = 0
• I₃ = -3 J₂ = 0
• J₃ = π³ - (-π)³ + 3 I₂ = 2π³ - 12π
• I₄ = -4 J₃ = -8π³ + 48π
When n = 0, the integral we care about is
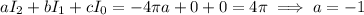
When n = 1,
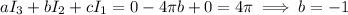
When n = 2,
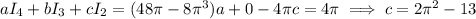
so that